Excerpts are particularly extensive because of the great significance of this book, and its particular relevance to the central argument of CAR. The quotes provide an exemplary model of inferential reasoning.
| Gaps in sequence |
p. 33 |
As was the case with the projective straight line, the developmental
sequence of the notion of regular cross section is far from complete. |
| No intermediate stage for straight edge |
p. 38f |
What is not clear is the development of these projective abilities. No
argument can be made for projective relations during the Oldowan.
No straight edges exist, and there are no intentionally regular cross
sections. The West Natron artifacts are more equivocal. Some are extensively trimmed, some have vaguely straight sides, and some of the
bifaces have somewhat regular cross sections. [...] In other words the
"intermediate" position of West Natron artifacts in regard to topological relations is not corroborated by their position in regard to projective relations. These appear to have been a relatively late addition
to the hominid repertoire. |
| Late date for euclidean concepts |
p. 39f |
The idea of space as a general
framework of positions is one that develops during ontogeny, and, as
I hope to show in this section, it appeared in the behavior of early
humans by 300,000 years ago. [...] there is early evidence
for a concept of measurement but not for one of parallel axes, a fact
that has interesting implications for the evolution of euclidean space. |
| Seriation problems |
p. 54f |
If we limit our consideration of symmetry to euclidean concepts of
congruency, perpendicular and bisected lines, and so on, then the
developmental sequence presented by stone tools consists of only two
stages - early stone tools for which an argument for symmetry cannot
be made, and later artifacts, like those from Isimila, for which it must
be made. This is not much of a sequence, and, in fact, it tells us nothing about the antecedents of euclidean notions, which is just what we
would like to know. |
| Overview |
p. 58 |
It seems that the development of a general frame of spatial
reference did not include an "affine" stage of competence in parallels,
but did include the relatively early appearance of notions of interval,
shape, and mirroring.
|
| Ape-like stage for Olduwan |
p. 63 |
Oldowan hominids attended to the nature of the edge - probably
tied to a specific task at hand - and paid no attention to the overall
shape of their tools. These edges required, as we have seen, only rudimentary spatial concepts. Indeed, in many respects these tools resemble tools made by modern chimpanzees. Both have simple modifications tied to an immediate task, and both are spatially simple. [...] in terms of spatial concepts, Oldowan
tools look very ape-like.
|
| Disregard for overall shape |
p. 23f. |
the knapper had to position the trimming blows in a
rudimentary series in which sequential blows were spatially related to
several preceding blows. This is a simple concept of order. All of these
Oldowan concepts of space are simple, and, interestingly, all appear
to be focused on the configuration of edges. There appear to have
been no ideas about appropriate overall shape, nor any spatial concepts used solely to control overall shape. [...] Notions of overall artifact shape appear after the Oldowan. [...] The minimally trimmed bifaces from Isimila [300,000 years ago] represent the most
sophisticated concepts of topological space. Here the knapper directed blows to achieve an overall shape in a very economical manner. |
| p. 60 |
There appears to have been little attention to the overall shape of
Oldowan tools. It was the configuration of edges that was the goal of
these stone knappers. [...] The hominids appear to have made no attempt to alter the overall
shape of the tools, for whatever reason. Such attention to overall
shape is a characteristic of succeeding technologies. |
| Appearance 1,200,000 years ago |
p. 61 |
Both the notion of interval and the notion of symmetry contributed
to the development of the idea of the
artifact as a whole. No longer did
hominids focus attention
only on the edge; they attempted
to attain certain overall shapes. Discoids, spheroids, and bifaces all required some notion of overall design. |
| Awareness of intended results |
p. 62 |
Like earlier hominids they had an idea of final
shape, but, unlike their earlier counterparts, they had a sophisticated
array of spatial concepts for conceiving and attaining the desired result. |
| A landmark (1,200,000 years ago) |
p. 63 |
Oldowan hominids attended to the nature of the edge - probably
tied to a specific task at hand - and paid no attention to the overall
shape of their tools. These edges required, as we have seen, only rudimentary spatial concepts. [...] The acquisition that first takes hominid tools out of range of ape
spatial concepts is the notion of overall shape, or, to put it a bit differently, some conception of the tool as a whole. While the edge-oriented
technology of the Oldowan appears to have been tied to immediate
tasks at hand (an ad hoc technology), the presence of tools with repeated, overall shape suggests that in these cases, an idea of the whole
tool existed previously in the mind of the knapper. [...] We do not know why these 1.2-million-year-old hominids strived to attain this particular shape, but
we do know some of the shape's conceptual requirements. With bifaces, the whole tool,
more or less, had to be conceived ahead of time. |
| Repetitive patterns |
p. 64 |
While the idea of artifact- or object-as-a-whole may seem painfully
rudimentary, it represents a much more comprehensive organization of space than that used in the Oldowan. Simple spatial notions
like order and separation had now become elements arranged into
higher-level patterns. Moreover, these patterns could be repeated
again and again because they existed as specific intentions. Technology could exist apart from a specific task at hand, and, indeed, had
come to occupy a conceptual realm of its own. |
| Importance of such ability |
p. 38 |
The ability to distinguish and coordinate independent perspectives
is an important
component of modern adult concepts of space. It is
commonplace for us to imagine how an object or scene will appear
from another perspective (we even use similar skills to measure intelligence on standard tests). It is an efficient and useful way to apprehend the world. Without this ability, the world would constantly present unfamiliar scenes. Even well-known objects would, if approached
or seen from a new angle, appear different because of the inability
to imagine how they would appear from the other, familiar angle. [...] projective notions [...] are important spatial notions.
Awareness of independent points of view implies that an individual
recognizes that both he and the object exist within a space of changing
relative positions. |
| Children know only their viewpoint |
p. 38 |
Young children do not possess this concept, and its absence yields an
interesting notion of space. For example, when presented objects arranged into a scene, young children consider the relative spatial position to be permanent; that is, they assume that the left-right and
front-back order that is visible from their perspective is the same for
all other observers. When asked to predict the shape of a shadow on
a screen, they describe the object as they see it from their own position. In other words, young children do not consider viewpoints other
than their own (Piaget and Inhelder 1967). |
| A landmark |
p. 64 |
The second constellation of spatial concepts includes euclidean and
projective notions, along with a more sophisticated understanding of
the relation or whole to parts. The acquisition of this constellation
appears to have hinged on a single breakthrough in spatial thinking -
the invention or discovery of perspective. This projective notion was
the key that allowed the extension of internal spatial frames that were
anchored to specific objects into general constructions of space that
organized possible as well as real positions. |
| A conceptual feat |
p. 64 |
As we can see
from the early bifaces from West Natron and Olduvai, a notion of
interval was in use fairly early, but there is no evidence of general
frames of reference. Intervals are, by themselves, insufficient. What
is required "as well is a constant orientation, and such constant orientation is impossible without some notion of viewpoints that exist independent of that of ego. One must be able to step away from the
tyranny imposed by direct perception and construct alternative views.
This is quite a conceptual feat, requiring complex substitutions and
restructuring of shapes. Moreover, it requires the subjugation of what
one actually sees to what one thinks. |
| Secondary trimming as indicative of intentionality |
p. 3 |
Much that is regular about stone tools is purely accidental. [...] Intention does not require some sophisticated image or mental template. [...] The analyses in this book concern, therefore, the
patterns of trimming found on tools. Occasionally they also consider
the overall shape of the artifact, but only in cases where it is clearly
the result of extensive trimming. |
p. 37 |
Without extensive trimming it is difficult to argue for any kind of intention. |
p. 39 |
It is the amount of trimming that makes me cautious; the
shape just might be fortuitous. |
p. 41 |
Moreover, neither artifact is extensively trimmed, making it hard to argue for an intentional shape.
[...] The disc shape is probably fortuitous. |
| Repetitive examples |
p. 4 |
I did try to avoid
unique examples. Even though a remarkable pattern or configuration
seemed, at least to me, certainly intentional, it remained just possible
that it was an accident. However, if this pattern was repeated on another artifact, I decided that the possibility of its being an accident
was reduced to an acceptably low level, and felt comfortable in including it in the sample. There are only two or three such unusual patterns in the study. |
| Symmetry |
p. 18 |
For objects such as the choppers
and scrapers of previous examples it is impossible to make judgments
about minimal trimming because we have little idea of the knapper's
intention concerning overall shape, if in fact he had one. But for artifacts with symmetry or regularity of any arbitrary kind we can make
such judgments, keeping in mind that they are, in fact, judgments. |
| Quick planning |
p. 19 |
[...] we need not envision the hominid in agonizing contemplation, but even quick, on-the-spot planning
required a notion of whole and part. |
| Caution |
p. 32 |
These examples are cautionary and I include
them to emphasize the care that must be taken in determining the
necessary competence of hominid stone knappers. Regularity in stone
tools can be accidental, and, moreover, even extensively trimmed artifacts can be irregular. |
p. 45 |
The same caveats hold when one examines stone tools for parallel
edges that hold when one inspects them for projective relations. It is
especially hard to prove intention. |
| Simple notions |
p. 40 |
The amount of trimming on this discoid suggests that the final
shape was probably intentional. [...] At the minimum, he must have used some concept of radius or diameter, that is some notion of a constant amount of space separating all of the edges. [...] I do not mean to argue that the knapper
was a geometrician and reflected upon such concepts, only that he
used a simple notion of interval in his spatial repertoire. |
| Insufficient evidence |
p. 52f. |
[...] there is nothing about
the location of trimming that suggests that the shape of the original
cobble was significantly altered. [...] In this case, the symmetry is in the
heads of the archaeologists. |
| No verbalization |
p. 57 |
Again I must emphasize that
the knapper need not have been able to describe or to verbalize his
concepts in nice mathematical terms. |
| No conscious theorizing |
p. 63 |
Like earlier hominids they had an idea of final
shape, but, unlike their earlier counterparts, they had a sophisticated
array of spatial concepts for conceiving and attaining the desired result. |
There is no specific discus
sion of structure in the book, but the central notion is implied by the following remarks.
| No analysis of structure per se |
p. 3 |
The analyses in this book concern, therefore, the
patterns of trimming found on tools. Occasionally they also consider
the overall shape of the artifact, but only in cases where it is clearly
the result of extensive trimming. |
| Sequential complexity [as a clue to structure] |
p. 12 |
Separation is the notion of distinguishing or segregating the elements in a spatial field so that each can have a specific,
rather than general, relation to the others. Order coordinates separation with proximity to create such concepts as the pair, the sequence,
and, most complex, the reversible sequence. |
| Non random sequence of blows |
p. 13 |
The knapper directed three specific blows (dissociation, separation) to a position adjacent to preceding blows (proximity). Indeed,
preceding negative scars appear to have supplied specific striking
platforms for subsequent blows. The result is not a random collection
of projections and edges but a single working edge. The minimum
necessary concept is that of the pair. |
| Relation of single constituents to the whole |
p. 15 |
Each flake is placed in relation not just to
another one but to all of the other flake scars. The knapper achieved
this result by restricting successive trimming blows to a single direction. This constant direction of movement is the third notion in a
concept of order. |
| p. 18 |
The final topological notion of use in analyzing stone tools is that
of continuity - the relationship of parts to a whole. A line is, topoIogically, an infinite series of indiscernably small points. In order to
conceive of a line in this fashion, it is necessary to be able to subdivide
the line infinitely and then recreate it in thought from the resulting
elements. Stated in another way, one must analyze a whole (the line)
into its constituent elements (the points) and resynthesize these elements into the whole. |
| p. 19 |
[...] we need not envision the hominid in agonizing contemplation, but even quick, on-the-spot planning
required a notion of whole and part. |
| Linear order |
p. 17 |
Put abstractly, we can argue for a concept of linear order. Each element, in
this case trimming flakes, was placed in relation to several other elements, the result being a sequence. |
| Potential elements of the whole |
p. 19 |
In order to have done this the knapper
needed some notion of the shape broken down into potential constituent elements, in this case trimming flakes, and of their combination
into the finished whole - in other words, a fairly sophisticated idea of
the spatial relation of parts to the whole. |
| Whole to parts, 300,000 years ago |
p. 62 |
the notion of
whole-part relations, the understanding of the spatial relationship of
a whole to its constituent parts. The minimally trimmed bifaces required an idea of final shape (which could include the euclidean
notions discussed above) and also an awareness of the minimum
modifications required to achieve that shape. The knapper had to
understand how each possible modification would affect the result, and
choose accordingly. Trial-and-error knapping, even with constant
checking, would be insufficient.
|
The term and the notion as such are missing in the book, but the ability to distinguish and to unite non contiguous elements (para-perception) is implied by the following.
| Analysis and synthesis |
p. 18 |
In order to
conceive of a line in this fashion, it is necessary to be able to subdivide
the line infinitely and then recreate it in thought from the resulting
elements. Stated in another way, one must analyze a whole (the line)
into its constituent elements (the points) and resynthesize these elements into the whole. It is a breaking down and putting back together
which, in terms of simpler topological relations, requires the coordination of proximity, separation, and order. Such whole-part relations
are among the most sophisticated of topological notions and, if we
can get at them, should be quite important in characterizing the spatial competence of early hominids. It is obviously impossible to see an
infinitely small point or to inquire about understandings of lines.
However, it is possible to examine the results of the process of analysis
and synthesis, the ability to break a whole into constituent elements
and put it back together again. |
| Coordinating viewpoints |
p. 28 |
As is true of the topological concept of analysis and synthesis,
there is good evidence for consideration of perspective in later Acheulean bifaces. This competence included not only the ability to operate from one stable viewpoint but the ability to coordinate viewpoints. This conclusion is corroborated by the evidence from cross
sections. |
| No standard modern typology |
p. 4 |
The analysis does not use any standard archaeological typology. I
do use some archaeological terms such as "scraper" and "handaxe"
but only as convenient terms of reference. The implied function in
such terms is irrelevant. Indeed, the purpose for which the hominid
made the tools is not at issue. [...] A hominid
could have made two tools with very different tasks in mind, but if he
used the same spatial notions to conceive both of them, then, from
the point of view of this analysis, the tools are equivalent. There is a
typology of sorts inherent in the analysis. It consists solely of spatial
relationships identified on the tools - proximity and symmetry, for
example. |
| No isolated assemblages of items that are based only on proximity |
p. 11 |
...
there is no known artifact assemblage that consists exclusively of unmodified flakes and single-blow cores. |
| p. 12 |
... there is no known assemblage that consists entirely of artifacts
of such simplicity. However, it is at least conceivable that an assemblage of such artifacts did in fact constitute the earliest recognizable
(though as yet unrecognized) set of stone tools. |
| Placing of blows on rough stone provides a firm clue to intention |
p. 10f |
In order to use topological concepts to analyze stone tools we must
ask what spatial notions (there had to be some!) the hominid knapper
used while striking one stone onto another. We cannot simply use the
geometry of the finished product, because almost every stone tool is
topologically equivalent – a three-dimensional solid equivalent to a
solid ball (the exceptions are stone rings found in some late assemblages). As a consequence we must step down and look at the arrangement of elements on the tool itself. Certain topological relations can
be apprehended from the way in which the knapper positioned trimming flakes during the manufacture of an artifact. In a very real
sense, the placing of trimming blows, particularly as they are positioned relative to previous ones, reflects concepts used by the knapper.
Three topological notions are especially evident in the trimming
patterns of stone tools: proximity, order, and continuity. These represent increasingly complex spatial coordinations. |
| Significance of contiguity |
p. 13 |
The result of contiguous
placing of trimming blows is a single prominent edge. One could argue that the flake scars of the previous examples of "proximity only"
artifacts (Figures 1 and 2) were also placed contiguously and hence
also represent a rudimentary concept of order. This is possible. However, there is nothing about these more primitive artifacts, such as one
prominent edge, that required a concept more sophisticated than simple proximity, and, to reiterate a crucial point, we can only argue
about minimum competence. |
##### 1. Proximity {#proximity}
| Applying the notion of proximity |
p. 10f |
Perhaps the most rudimentary spatial concept is that of proximity –
the perceiving or placing of elements in the same spatial field. It is
simply a notion of "nearness" or "byness," and is so basic that virtually
every trimmed artifact is equivalent to every other trimmed artifact.
Each trimming blow is in some sense "near" the others on the artifact.
The only exceptions are unmodified flakes and cores that have had
only one trimming blow or, perhaps, two unrelated trimming blows,
though it would be difficult if not impossible to prove that the second
trimming flake was not placed somehow near the first. From the perspective of this simple spatial notion all trimmed stone artifacts, from
polyhedrons to fine bifacial points, are equivalent because multiple
trimming flakes have been placed in proximity to one another. Now
there is no known artifact assemblage that consists exclusively of unmodified flakes and single-blow cores.
Competence in proximity is,
therefore, a kind of base point from which we can begin to describe
the evolution of spatial concepts. As it turns out, there are artifacts
whose knapper need only have used a notion of proximity. The following examples are from Bed I at Olduvai. |
| Specific examples |
p. 10f |
Figure 1 (FLK N). To have made this artifact, the stone knapper
need only have struck the cobble repeatedly in the same general vicinity. It was not necessary that he place one blow in some precise
relationship to a previous one, only that the blows be more or less
near one another. The result was a number of sharp projections and
edges that would probably have been useful for several kinds of tasks.
Figure 2 (DK). At first glance this artifact may appear somewhat
more sophisticated than the preceding. There are more trimming
flakes, removed by blows from several different angles. Simple bashing would not suffice. Because we can only argue about minimum
competence, though, we must conclude that this artifact could have
been manufactured by someone who simply placed his trimming
blows near other trimming blows.
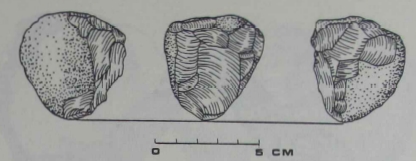
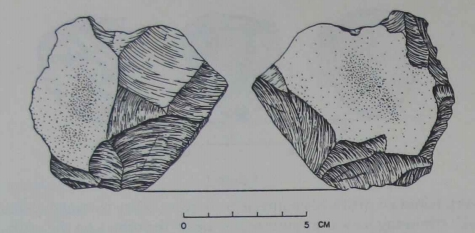
Figure 1 Figure 2
|
##### 2. Order – pairing {#order-pairing}
| Applying the notion of pair |
p. 12 |
Separation is the notion of distinguishing or segregating the elements in a spatial field so that each can have a specific,
rather than general, relation to the others. Order coordinates separation with proximity to create such concepts as the pair, the sequence,
and, most complex, the reversible sequence.
In a pair, proximity and separation are coordinated but there is no
need for a constant direction of movement. The elements in a pair
must be distinct yet contiguous, hence the coordination of separation
and proximity. |
| Separation |
p. 23 |
If the hominid wanted to make a tool with a single edge,
however, proximity alone would not suffice. He would need a concept
of separation, in which the edge acts as a kind of boundary or reference separating faces of the tool. He would have to direct his blows
with regard to that boundary; this concept is more complex than simple proximity. |
| Specific examples
|
p. 12f |
Figure 3. [...] Four
trimming blows have produced a single sharp edge along about one third of the circumference of a cobble. Trimming flakes A and B preceded trimming flakes C and D. In effect, the artifact is the result of
two pairs of trimming blows. The order of the blows within each pair
is irrelevant, as is the order of the pairs to one another. Again, I am
emphasizing how the knapper had to place trimming blows to achieve
the result. Bashing in a general vicinity would not have been sufficient. The knapper directed three specific blows (dissociation, separation) to a position adjacent to preceding blows (proximity). Indeed,
preceding negative scars appear to have supplied specific striking
platforms for subsequent blows. The result is not a random collection
of projections and edges but a single working edge. The minimum
necessary concept is that of the pair.
Figure 5. This chopper has at least eleven trimming flakes
and, at first glance, appears more sophisticated than the preceding
two examples. In addition to simple pairs, the single edge on this
chopper required that the concept of separation incorporate several
elements. This pattern is intuitively more complicated than that of the
simple pair. In mathematical topology, separation is often exemplified by points positioned on opposite sides of a boundary of some sort
(inside or outside a circle, for example). On the chopper in Figure 5,
the knapper produced a sinuous edge by trimming onto two faces of
a cobble. True, the placing of each blow required the idea of a pair in
space. But the notion of a single edge also acted as a kind of boundary
separating the blows from each face of the tool. What makes this more
sophisticated than a simple pair is that the boundary - the edge - had
to have been maintained for several trimming blows. This boundary
was a spatial reference used by the knapper to orient his blows. The
concept of a simple pair was not quite sufficient.
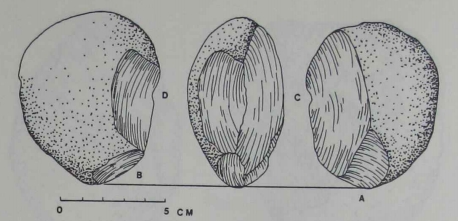
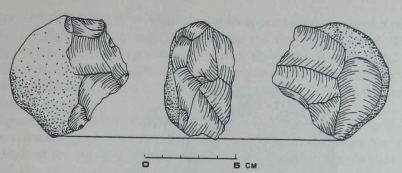
Figure 3 Figure 5
|
##### 3. Order – ordered sequence {#order-sequence}
| The notion of ordered sequence |
p. 14f. |
The notion of an ordered sequence requires the coordination of
proximity and separation with the addition of a constant direction of
movementor orientation. A pair is a pair regardless of the directional
orientation of the second element to the first. But if we want to create
a series of elements, such as a line of posts, we must employ some
concept in addition to separation and nearness. We must place the
third element and all subsequent elements in some specific spatial relation to all of the preceding elements. We cannot simply place the
third post near the second; we must also consider the position of the
first. This is most easily done by maintaining a constant direction
of movement. This coordination is more complex than that of the
pair because several distinct elements (separation) must be related
through some concept of arrangement, even one as simple as "move
to the left". |
| Specific examples
|
p. 14-17 |
|
Figure 6a (FLK N). In the view shown here, the lower edge of the
artifact consists of a series of six unifacial flake scars. On close examination one can see that the knapper did not strike off the trimming
flakes one after another in exact sequence (at least one is out of place;
see arrow). Consequently, any comparison to a strict sequence such
as ABCDEF would be spurious. Nevertheless, the end result is the
same - one flake scar following another. The violation of a strict order should not be disturbing. It is unlikely that these early hominids
played logical games with themselves, at least using stone tools.
|

|
The
coordination of proximity and order in this artifact is certainly more
complex than that of a pair. Each flake is placed in relation not just to
another one but to all of the other flake scars. The knapper achieved
this result by restricting successive trimming blows to a single direction. This constant direction of movement is the third notion in a
concept of order.
Figure 6b. This
example differs from earlier ones in that it is a flake
tool; that is, the
blank itself was a flake rather than a cobble or a chunk of stone. This
implies two major manufacturing steps - the removal of the flake
from a core and the subsequent trimming of the flake. While this
increase in number of steps reflects a greater complexity of sorts, it is
of no direct relevance to a discussion of spatial concepts, especially
since we have no way of knowing whether the whole sequence was
conceived at the outset or whether the knapper simply selected a previously struck flake as most appropriate for the task at hand. The
spatial concepts necessary for trimming this flake are identical to
those used on the cobble in the preceding example.
Figure 6c. This small scraper was also made on a flake.
The trimming flakes are related to one another in the same manner
as those of the two preceding examples. What is important here is the
small size of the trimming flakes; the knapper needed a fairly fine
motor control to make this artifact. The "primitiveness" of Oldowan
tools cannot, therefore, be explained in terms of poor motor coordination on the part of the hominids.
In makingthese three artifacts, Oldowan hominids employed a spatial concept more sophisticated than that of a simple pair. Put abstractly, we can argue for a concept of linear order. Each element, in
this case trimming flakes, was placed in relation to several other elements, the result being a sequence. Though their order was not as
elegant as a purely mathematical series such as ABCDEF, it is still
clear that these hominids were capable of arranging a sequence of
elements.
|
##### 4. Order – reversed sequence {#order-reversal}
| The notion of reversed sequence (symmetry) |
p. 17 |
[...] there
are some kinds of artifacts that required a reversal, though the spatial
elements were more abstract than simple trimming flakes. I am referring, of course, to bifaces, whose bilateral symmetry requires the reversal of order around a midline. ABC/CBA is a symmetry. |
#### Continuity {#continuity}
| Breaking down and putting back together
|
p. 18 |
[ ] the relationship of parts to a whole. A line is, topologically, an infinite series of indiscernably small points. In order to
conceive of a line in this fashion, it is necessary to be able to subdivide
the line infinitely and then recreate it in thought from the resulting
elements. Stated in another way, one must analyze a whole (the line)
into its constituent elements (the points) and resynthesize these elements into the whole. It is a breaking down and putting back together
which, in terms of simpler topological relations, requires the coordination of proximity, separation, and order. Such whole-part relations
are among the most sophisticated of topological notions and, if we
can get at them, should be quite important in characterizing the spatial competence of early hominids.
[A relatively late development: the book discusses at this point the question of possible transitional items.] |
| intention |
p. 18 |
For objects such as the choppers
and scrapers of previous examples it is impossible to make judgments
about minimal trimming because we have little idea of the knapper's
intention concerning overall shape, if in fact he had one. But for artifacts with symmetry or regularity of any arbitrary kind we can make
such judgments, keeping in mind that they are, in fact, judgments |
| Example |
p. 19 |
| The symmetry of this particular biface resulted from four short sections of trimming (A, B, C, and D) that are, for the most part, unconnected with each other. In order to have done this the knapper
needed some notion of the shape broken down into potential constituent elements, in this case trimming flakes, and of their combination
into the finished whole - in other words, a fairly sophisticated idea of
the spatial relation of parts to the whole. |
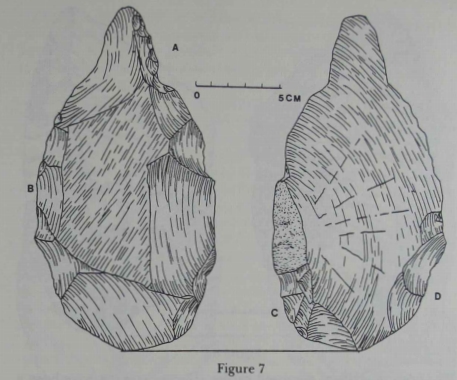
|
Only by reducing the shape
to potential trimming flakes could he have determined which were
necessary and which were not. Again, we need not envision the hominid in agonizing contemplation, but even quick, on-the-spot planning
required a notion of whole and part.
|
#### Projective concepts {#projective}
Definition:
constancy of items in spite of change in perspective |
p. 24 |
Projective geometry is a geometry of viewpoints or perspectives. It
is concerned with qualities of figures that remain constant when the
source of a projection changes. A simple way to explore projective
relations is to study changes in shadows cast by a point source such as
a candle or flashlight. One can easily transform the shadow of a
square piece of cardboard into a rhombus or a trapezoid, but it is impossible to change the shadow into a triangle or a circle. Some qualities of the figure remain constant regardless of its relation to the light
source. |
| Must be argued from within the object |
p. 25 |
We are interested
in intuitive notions of space and, in particular, in how these intuitive
notions govern the manufacture of stone tools. The intuitive notion
of perspective is therefore of some interest. Do any patterns displayed
by stone tools require concepts that include some consideration of
perspective, that is, that consider the relative orientation of object and
observer? [...] We are left
again with patterns internal to stone tools, and only a few of these
suggest specific projective notions. The most notable are intentional
straight edges and regular cross sections. |
| Must be argued from within the object |
p. 28 |
As is true of the topological concept of analysis and synthesis,
there is good evidence for consideration of perspective in later Acheulean bifaces. This competence included not only the ability to operate from one stable viewpoint but the ability to coordinate viewpoints. This conclusion is corroborated by the evidence from cross
sections. |
| MInimum necessary competence |
p. 33 |
Unless the artifact is extensively trimmed and extremely regular, it is difficult, if not impossible, to document projective relations. The minimum necessary
competence does not, therefore, include projective notions. |
#### Straight line {#straight}
| Definition |
p. 25f. |
When the position of the observer is taken into account, certain
spatial qualities are added to the simpler topological ones. A straight
line viewed from the proper position becomes a point (the terminal
point of a straight line is capable of masking all of the other points),
but there is no position from which a curved line can be seen as a
point. The ability to create a straight line presupposes an awareness of this stable viewpoint, either by actual sighting or by imagination. [...] What is true of projective straight lines must also be true of straight
aspects of artifacts, but only if the straightness is clearly the result of
intentional modification. [...] Much that is straight on stone tools is a result
of manufacture on flakes, many of whose natural edges approach
straightness. |
Example:
|
p. 26 |
| The trimmed lateral edge of this
cleaver is remarkably straight, and, more important, the extent of the
trimming suggests that the original shape of the edge was considerably altered. The edge is also straight in profile. This required the
knapper to control two viewpoints or perspectives at the same time.
Competence in the basic topological notions discussed in the previous
chapter would not |
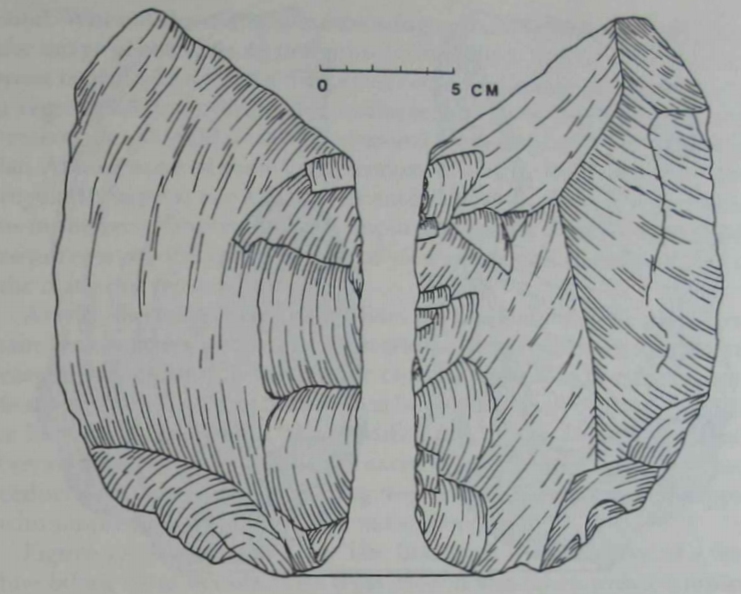
|
have been sufficient. The knapper had to have
related the trimming of the edge to a constant point of view. Moreover, because the edge is also straight in profile, the knapper had to
have considered a point of view located on another plane. Even if the
knapper continually checked the edge by actual sighting, he had to be
aware that the shape varied according to the viewpoint, that what was
straight from one sighting point was perhaps not straight from another. In other words, some notion of perspective must have been
present in the knapper's spatial repertoire, and a fairly sophisticated
one at that since there are two coordinated perspectives evident here.
|
#### Cross section {#cross}
| Definition |
p. 28 |
The cross section of an object is the two-dimensional shape produced by a plane intersecting the solid. For example, the cross section
of a sphere is a circle; of a cylinder, a circle or an ellipse; of a pyramid,
a rectangle. The cross section of a biface is the two-dimensional shape
produced by an imaginary plane intersecting the artifact. We say that
a biface has a "regular" cross section if it presents a recognizable twodimensional figure such as a rhombus or a triangle or a lens shape.
Symmetry is usually the most telling quality of regularity. |
| Imagination |
p. 28f. |
The ability to conceive of and create a regular cross section requires
a sophisticated coordination of viewpoints or perspectives. First, it is
necessary that the observer – in our case the knapper – be aware of a
viewpoint that is not actually available to him. One cannot sight into a solid. Without the aid of some assisting apparatus such as a template the image of the cross section must be imagined.
Second, the observer must coordinate a virtual infinity of cross sections or perspectives. |
Example
|
p. 29 |
| The cross section was taken with a template
at the point of maximum width. As can be seen from Figure 13, the
artifact is extensively trimmed, and it is fair to conclude that the original shape of the blank, including the cross section, has been changed.
Could the knapper have controlled the shape of this cross section by
directly sighting from a perspective to the rear of the artifact? Such a
direct sighting would actually combine (and confound) the dimensions of maximum width and maximum thickness, which do not fall
at the same point on the length of the artifact (maximum thickness is
farther toward the tip). In other words, the knapper would see a
"view" that was a composite of two separate cross sections. |
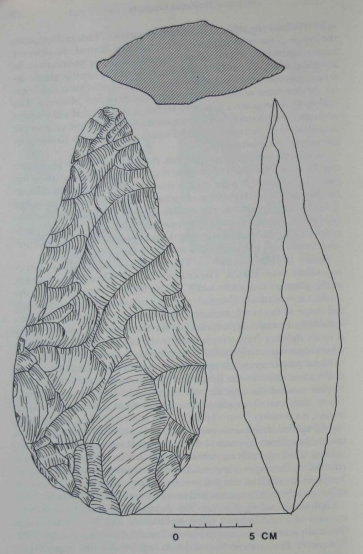
|
There is,
in fact, no position from which the cross section of the artifact in Figure 13 can be directly observed. It must be created in the imagination
or, as I have done, measured with a device. Moreover, a planar intersection taken virtually anywhere on this artifact, even at angles not
parallel to the major axes, would yield a regular cross section. The
knapper constructed not just one imaginary viewpoint but a virtual
infinity of them. His control in this regard was quite remarkable.
|
| Reversal and congruency |
p. 51 |
[The item in Figure 13] is not only bilaterally symmetrical in plan, it is symmetrical
in profile and in all of its cross sections. Furthermore it is extensively
trimmed, and the shapes are certainly intentional. The symmetry is
extremely regular, and the mirrored shapes are congruent. One
could improve little on the result if one were to use a measuring device. The symmetries in this artifact come very close to fulfilling the
formal definition of symmetry. |
| End point of developmental sequence |
p. 52 |
The handaxe in Figure 13 also suggests something even more remarkable than simple bilateral symmetry. The artifact demonstrates
symmetry across not just a midline in plan, but also a midline in profile and a midline for all of the cross sections. These lines intersect to
define a three-dimensional space, intuitively equivalent to a space of
Cartesian coordinates. It is difficult to imagine how a more sophisticated conception of space could be employed in stone knapping. Artifacts like this one constitute the endpoint of our developmental
sequence. |
| Three-dimensional frame of reference |
p. 57 |
The fine bifaces, like those in example 13, have
bilateral symmetry in three dimensions (as we would define them).
The knapper had to be able to invert
congruent shapes across an
imaginary midline for three separate dimensions and to coordinate
them. This required a frame of reference of considerable complexity,
and, while I suppose it possible that this frame was applied only to
spatial relations on or within artifacts, this seems to me very unlikely.
The abstract nature of such a spatial framework suggests that it was a
general one, extendable to all of space. Again I must emphasize that
the knapper need not have been able to describe or to verbalize his
concepts in nice mathematical terms. That he employed such a framework, however, is, I think, undeniable. |
#### Euclidean concepts {#euclidean}
| Definition |
p. 39 |
the development of general constructions of space, spatial notions
that transcend individual objects and their relations and organize
space into a framework in which objects occupy positions.
A euclidean space is one of positions, not of objects. It is defined by
an arbitrary framework, a set of coordinates, for example. In a sense,
one empties space of objects and organizes what is left by means of a
reference system that consists of all of the potential positions objects
may hold. |
| Units of consistent spatial quantity |
p. 39 |
Such a space requires intervals, which are units of consistent spatial quantity. Amount of space is irrelevant to topological and projective space, but it is one of the key concepts around which euclidean space is built. Spatial intervals act as an independent and constant reference against which objects can be compared and located
in space.
|
| A space of positions |
p. 39 |
A space of positions is the space in which modern adults habitually
act and think. Whether or not it is consciously thought of as a threedimensional coordinate grid, the everyday world (the life-world of
phenomenologists) is acted upon as if space were a given and immutable entity in which objects occupied positions. However, "... it
would be a complete mistake to imagine that human beings have some
innate or psychologically precocious knowledge of the spatial surround organized in a two- or three-dimensional reference frame"
(Piaget and Inhelder 1967:416).
|
#### Measurements {#measurement}
| Definition |
p. 40 |
any notion of a relatively
constant amount of space used as a reference of some sort. This need
not be a formally defined idea of meters or inches, but could be
such readily available references as hand breadth and literal feet. Of
course, it would be difficult to document the use of such intervals in
prehistory. However, there are two constant intervals that appear to
have been used fairly early in the manufacture of some stone tools –
the radius and diameter. [...] The interval of a radius is not general, but is specific to a
particular tool. Nevertheless, it is an interval that consists, however
briefly, of a constant quantity of space. |
The notion of interval
|
p. 40 |
There are two constant intervals that appear to
have been used fairly early in the manufacture of some stone tools –
the radius and diameter. [...] The interval of a radius is not general, but is specific to a
particular tool. Nevertheless, it is an interval that consists, however
briefly, of a constant quantity of space. |
| p. 45 |
I do not wish to overemphasize the importance of a concept of interval. It is not in and of itself evidence for a competence in euclidean
space. However, the notion of a quantity of space is one of the prerequisites to euclidean concepts, and here we have it, in rudimentary
form perhaps, in the regular diameters of upper Bed IIdiscoids and
spheroids.
|
Example:
discoids
|
p. 40 |
| Figure 20. The amount of trimming on this discoid suggests that the final
shape was probably intentional. The rudimentary spatial notions of
order and separation are insufficient to explain this artifact; the knapper |
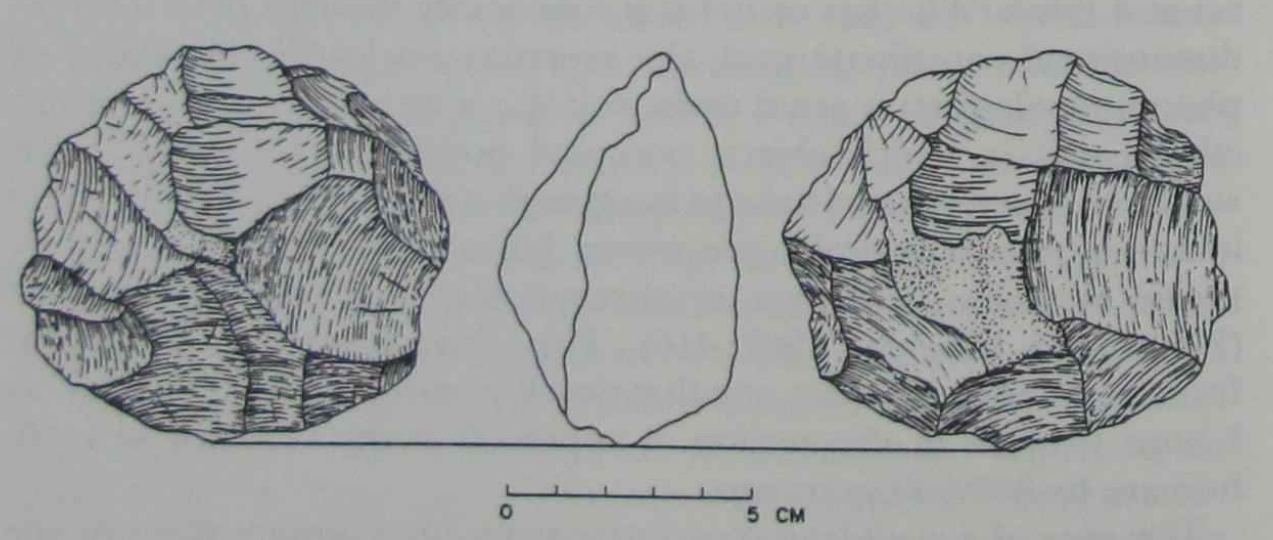 |
must have employed some additional spatial concept. At the minimum, he must have used some concept of radius or diameter, that is some notion of a constant amount of space separating all of the edges.
Alternatively, he might have used some idea of a regular curve employing a reference system of chords and arcs. But this is even more
complex than a radius. We may conclude that the knapper of this
discoid used some notion of interval, either radius or diameter, while
making this artifact. Again, I do not mean to argue that the knapper
was a geometrician and reflected upon such concepts, only that he
used a simple notion of interval in his spatial repertoire. |
#### Parallel axes {#parallel}
| Parallel axes and "affine" geometry |
p. 45 |
A second spatial notion that is an element of euclidean space is that
of parallel axes, which are essential to the formal definition of a coordinate grid. Actually, parallels constitute a geometry all their own,
termed "affine" geometry, with its own set of axioms and theorems.
While it is possible to define parallel lines using euclidean notions of
angles and measurement, it is not necessary to do so. Any two lines
on a plane that never meet are parallel. This definition assumes a
concept of plane, but in practice is well within the competence of an
intuitive geometry. This does not mean, however, that it must exist as
an independent notion in an intuitive conception of space, nor that it
must precede a truly euclidean geometry in a developmental sequence. |
| p. 48 |
This argument about affine geometry may appear, I admit, rather
like sophistry. But it does bear on two important aspects of our
problem – the antecedents of euclidean concepts and the relation between developmental and "logical" sequences. The lack of an affine
"stage" will turn out to be quite important. |
| Example |
p. 45 |
| Figure 22 (Isimila). The lateral edges of this cleaver are extensively
trimmed, and it is fair to assume that the overall shape was intentional. The parallel here is about as good as one could hope to achieve
by bifacial trimming. This artifact actually approaches being a regular
quadrilateral. But does it exemplify a notion of parallel, or is the parallel just a side effect of bilateral symmetry, which is not an affine
concept? |
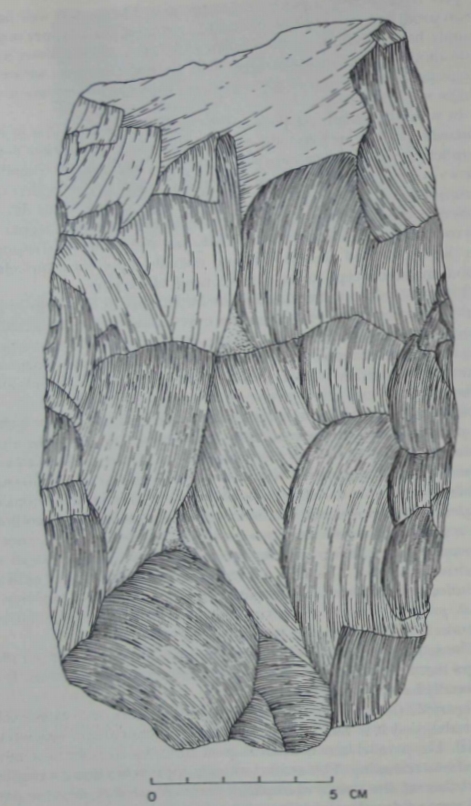 |
|
| Caveats |
p. 47 |
Based on artifacts such as these, an argument could be made that
the Isimila hominids had some concept of parallel in their spatial repertoire. However, there need not have been a concept of parallel that
was separate from euclidean notions of space since, as we shall see,
there are euclidean notions such as congruency that were used by the
Isimila hominids. To document a separate use of affine spatial relations, we would need an assemblage in which affine but not euclidean
relations were required. To my knowledge no such assemblage exists. |
#### Bilateral symmetry {#bilateral}
| Definition |
p. 49 |
Bilateral symmetry in its strict sense is a euclidean concept. "Two
points are said to be symmetrical with respect to a point, P, if P bisects the line segment joining the two points. Two figures can be considered symmetrical with respect to a point (line) if each point in
one figure has a symmetrical point in the other drawing" [...] In the case of symmetry with respect
to a line (bilateral symmetry), the bisecting line must be perpendicular
to the segment joining any two symmetrical points. The notions of
"bisect" and "perpendicular" require the quantitative concepts of
angle and distance (concepts of rotational and linear measurement).
A simpler intuitive notion of symmetry consists of mirror images, one
an exact but reversed duplicate of the other. Yet even here the idea
of an exact duplicate usually means a congruency, which is of course
a euclidean notion requiring conserved amounts of space and angle. |
| Reversal and congruency |
p. 50 |
In this section I will examine the development of bilateral symmetry by citing examples of artifacts that required a reversal about a
perpendicular bisecting line (which I will simply term a midline) as
well as some notion of symmetrical congruency, that is, the theoretical
infinity of symmetrical points that constitute symmetrical figures. |
| Example |
p. 50f |
| An even more powerful argument for a concept of symmetry can
be based on minimally trimmed artifacts.
Figure 26 (Isimila). The trimming at A especially suggests attention
to mirroringa congruent shape. The bit has been "pulled in" for the
same distance on the retouched margin as it was naturally done on
the opposite margin. The subsequent constriction extends for the same length along each side. The knapper also trimmed the butt into |
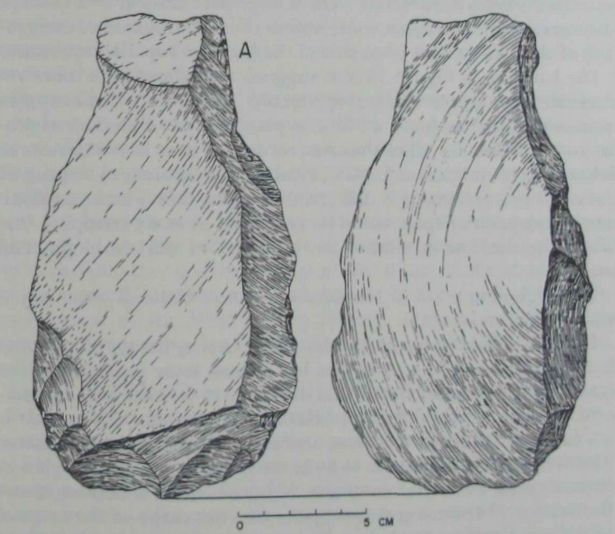 |
an even curve, giving the ardfact an excellent symmetry in plan with
minimal effort. The biface discussed earlier in Figure 7 presents a
similar approach to achieving symmetry. Both of these artifacts argue
for a concept of the relation between whole and parts. They also suggest that the conceived "whole" was in large part defined by a concept
of symmetry. In both cases, some notion of mirroring and of congruency of shape must have been part of the knapper's spatial repertoire.
|
Back to top: Thomas Wynn










