Back to top: Topological concepts
Proximity
| Placing of blows on rough stone provides a firm clue to intention | p. 10f | In order to use topological concepts to analyze stone tools we must ask what spatial notions (there had to be some!) the hominid knapper used while striking one stone onto another. We cannot simply use the geometry of the finished product, because almost every stone tool is topologically equivalent – a three-dimensional solid equivalent to a solid ball (the exceptions are stone rings found in some late assemblages). As a consequence we must step down and look at the arrangement of elements on the tool itself. Certain topological relations can be apprehended from the way in which the knapper positioned trimming flakes during the manufacture of an artifact. In a very real sense, the placing of trimming blows, particularly as they are positioned relative to previous ones, reflects concepts used by the knapper. Three topological notions are especially evident in the trimming patterns of stone tools: proximity, order, and continuity. These represent increasingly complex spatial coordinations. |
| Significance of contiguity | p. 13 | The result of contiguous placing of trimming blows is a single prominent edge. One could argue that the flake scars of the previous examples of "proximity only" artifacts (Figures 1 and 2) were also placed contiguously and hence also represent a rudimentary concept of order. This is possible. However, there is nothing about these more primitive artifacts, such as one prominent edge, that required a concept more sophisticated than simple proximity, and, to reiterate a crucial point, we can only argue about minimum competence. |
| Applying the notion of proximity | p. 10f | Perhaps the most rudimentary spatial concept is that of proximity –
the perceiving or placing of elements in the same spatial field. It is
simply a notion of "nearness" or "byness," and is so basic that virtually
every trimmed artifact is equivalent to every other trimmed artifact.
Each trimming blow is in some sense "near" the others on the artifact.
The only exceptions are unmodified flakes and cores that have had
only one trimming blow or, perhaps, two unrelated trimming blows,
though it would be difficult if not impossible to prove that the second
trimming flake was not placed somehow near the first. From the perspective of this simple spatial notion all trimmed stone artifacts, from
polyhedrons to fine bifacial points, are equivalent because multiple
trimming flakes have been placed in proximity to one another. Now
there is no known artifact assemblage that consists exclusively of unmodified flakes and single-blow cores. Competence in proximity is, therefore, a kind of base point from which we can begin to describe the evolution of spatial concepts. As it turns out, there are artifacts whose knapper need only have used a notion of proximity. The following examples are from Bed I at Olduvai. |
| Specific examples | p. 10f |
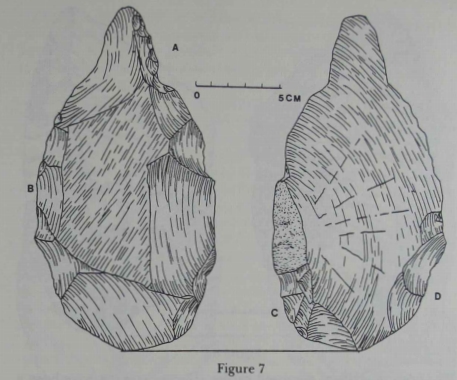
Figure 1 (FLK N). To have made this artifact, the stone knapper
need only have struck the cobble repeatedly in the same general vicinity. It was not necessary that he place one blow in some precise
relationship to a previous one, only that the blows be more or less
near one another. The result was a number of sharp projections and
edges that would probably have been useful for several kinds of tasks. Figure 2 (DK). At first glance this artifact may appear somewhat more sophisticated than the preceding. There are more trimming flakes, removed by blows from several different angles. Simple bashing would not suffice. Because we can only argue about minimum competence, though, we must conclude that this artifact could have been manufactured by someone who simply placed his trimming blows near other trimming blows. 
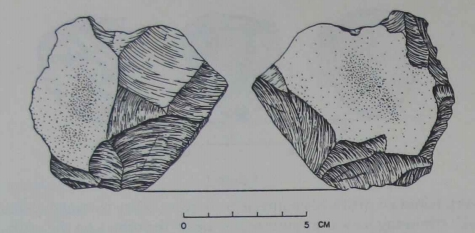 Figure 1 Figure 2 |
Back to top: Topological concepts
Order – pairing
| Applying the notion of pair | p. 12 | Separation is the notion of distinguishing or segregating the elements in a spatial field so that each can have a specific, rather than general, relation to the others. Order coordinates separation with proximity to create such concepts as the pair, the sequence, and, most complex, the reversible sequence. In a pair, proximity and separation are coordinated but there is no need for a constant direction of movement. The elements in a pair must be distinct yet contiguous, hence the coordination of separation and proximity. |
| Separation | p. 23 | If the hominid wanted to make a tool with a single edge, however, proximity alone would not suffice. He would need a concept of separation, in which the edge acts as a kind of boundary or reference separating faces of the tool. He would have to direct his blows with regard to that boundary; this concept is more complex than simple proximity. |
| Specific examples | p. 12f |
Figure 3. [...] Four
trimming blows have produced a single sharp edge along about one third of the circumference of a cobble. Trimming flakes A and B preceded trimming flakes C and D. In effect, the artifact is the result of
two pairs of trimming blows. The order of the blows within each pair
is irrelevant, as is the order of the pairs to one another. Again, I am
emphasizing how the knapper had to place trimming blows to achieve
the result. Bashing in a general vicinity would not have been sufficient. The knapper directed three specific blows (dissociation, separation) to a position adjacent to preceding blows (proximity). Indeed,
preceding negative scars appear to have supplied specific striking
platforms for subsequent blows. The result is not a random collection
of projections and edges but a single working edge. The minimum
necessary concept is that of the pair. Figure 5. This chopper has at least eleven trimming flakes and, at first glance, appears more sophisticated than the preceding two examples. In addition to simple pairs, the single edge on this chopper required that the concept of separation incorporate several elements. This pattern is intuitively more complicated than that of the simple pair. In mathematical topology, separation is often exemplified by points positioned on opposite sides of a boundary of some sort (inside or outside a circle, for example). On the chopper in Figure 5, the knapper produced a sinuous edge by trimming onto two faces of a cobble. True, the placing of each blow required the idea of a pair in space. But the notion of a single edge also acted as a kind of boundary separating the blows from each face of the tool. What makes this more sophisticated than a simple pair is that the boundary–the edge–had to have been maintained for several trimming blows. This boundary was a spatial reference used by the knapper to orient his blows. The concept of a simple pair was not quite sufficient. 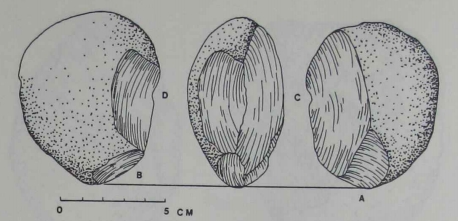
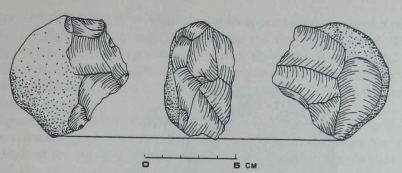 Figure 3 Figure 4 |
Back to top: Topological concepts
Order – ordered sequence
| The notion of ordered sequence | p. 14f. | The notion of an ordered sequence requires the coordination of proximity and separation with the addition of a constant direction of movementor orientation. A pair is a pair regardless of the directional orientation of the second element to the first. But if we want to create a series of elements, such as a line of posts, we must employ some concept in addition to separation and nearness. We must place the third element and all subsequent elements in some specific spatial relation to all of the preceding elements. We cannot simply place the third post near the second; we must also consider the position of the first. This is most easily done by maintaining a constant direction of movement. This coordination is more complex than that of the pair because several distinct elements (separation) must be related through some concept of arrangement, even one as simple as "move to the left". | ||
| Specific examples | p. 14-17 |
Figure 6b. This example differs from earlier ones in that it is a flake tool; that is, the blank itself was a flake rather than a cobble or a chunk of stone. This implies two major manufacturing steps–the removal of the flake from a core and the subsequent trimming of the flake. While this increase in number of steps reflects a greater complexity of sorts, it is of no direct relevance to a discussion of spatial concepts, especially since we have no way of knowing whether the whole sequence was conceived at the outset or whether the knapper simply selected a previously struck flake as most appropriate for the task at hand. The spatial concepts necessary for trimming this flake are identical to those used on the cobble in the preceding example. Figure 6c. This small scraper was also made on a flake. The trimming flakes are related to one another in the same manner as those of the two preceding examples. What is important here is the small size of the trimming flakes; the knapper needed a fairly fine motor control to make this artifact. The "primitiveness" of Oldowan tools cannot, therefore, be explained in terms of poor motor coordination on the part of the hominids. In makingthese three artifacts, Oldowan hominids employed a spatial concept more sophisticated than that of a simple pair. Put abstractly, we can argue for a concept of linear order. Each element, in this case trimming flakes, was placed in relation to several other elements, the result being a sequence. Though their order was not as elegant as a purely mathematical series such as ABCDEF, it is still clear that these hominids were capable of arranging a sequence of elements. |
Back to top: Topological concepts
Order – reversed sequence
| The notion of reversed sequence (symmetry) | p. 17 | [...] there are some kinds of artifacts that required a reversal, though the spatial elements were more abstract than simple trimming flakes. I am referring, of course, to bifaces, whose bilateral symmetry requires the reversal of order around a midline. ABC/CBA is a symmetry. |
Back to top: Topological concepts