Back to top: Euclidean concepts
Euclidean concepts
| Definition |
p. 39 |
the development of general constructions of space, spatial notions
that transcend individual objects and their relations and organize
space into a framework in which objects occupy positions.
A euclidean space is one of positions, not of objects. It is defined by
an arbitrary framework, a set of coordinates, for example. In a sense,
one empties space of objects and organizes what is left by means of a
reference system that consists of all of the potential positions objects
may hold. |
| Units of consistent spatial quantity |
p. 39 |
Such a space requires intervals, which are units of consistent spatial quantity. Amount of space is irrelevant to topological and projective space, but it is one of the key concepts around which euclidean space is built. Spatial intervals act as an independent and constant reference against which objects can be compared and located
in space.
|
| A space of positions |
p. 39 |
A space of positions is the space in which modern adults habitually
act and think. Whether or not it is consciously thought of as a threedimensional coordinate grid, the everyday world (the life-world of
phenomenologists) is acted upon as if space were a given and immutable entity in which objects occupied positions. However, "... it
would be a complete mistake to imagine that human beings have some
innate or psychologically precocious knowledge of the spatial surround organized in a two- or three-dimensional reference frame"
(Piaget and Inhelder 1967:416).
|
Back to top: Euclidean concepts
Measurement
| Definition |
p. 40 |
any notion of a relatively
constant amount of space used as a reference of some sort. This need
not be a formally defined idea of meters or inches, but could be
such readily available references as hand breadth and literal feet. Of
course, it would be difficult to document the use of such intervals in
prehistory. However, there are two constant intervals that appear to
have been used fairly early in the manufacture of some stone tools –
the radius and diameter. [...] The interval of a radius is not general, but is specific to a
particular tool. Nevertheless, it is an interval that consists, however
briefly, of a constant quantity of space. |
The notion of interval
|
p. 40 |
There are two constant intervals that appear to
have been used fairly early in the manufacture of some stone tools –
the radius and diameter. [...] The interval of a radius is not general, but is specific to a
particular tool. Nevertheless, it is an interval that consists, however
briefly, of a constant quantity of space. |
| p. 45 |
I do not wish to overemphasize the importance of a concept of interval. It is not in and of itself evidence for a competence in euclidean
space. However, the notion of a quantity of space is one of the prerequisites to euclidean concepts, and here we have it, in rudimentary
form perhaps, in the regular diameters of upper Bed IIdiscoids and
spheroids.
|
Example:
discoids
|
p. 40 |
| Figure 20. The amount of trimming on this discoid suggests that the final
shape was probably intentional. The rudimentary spatial notions of
order and separation are insufficient to explain this artifact; the knapper |
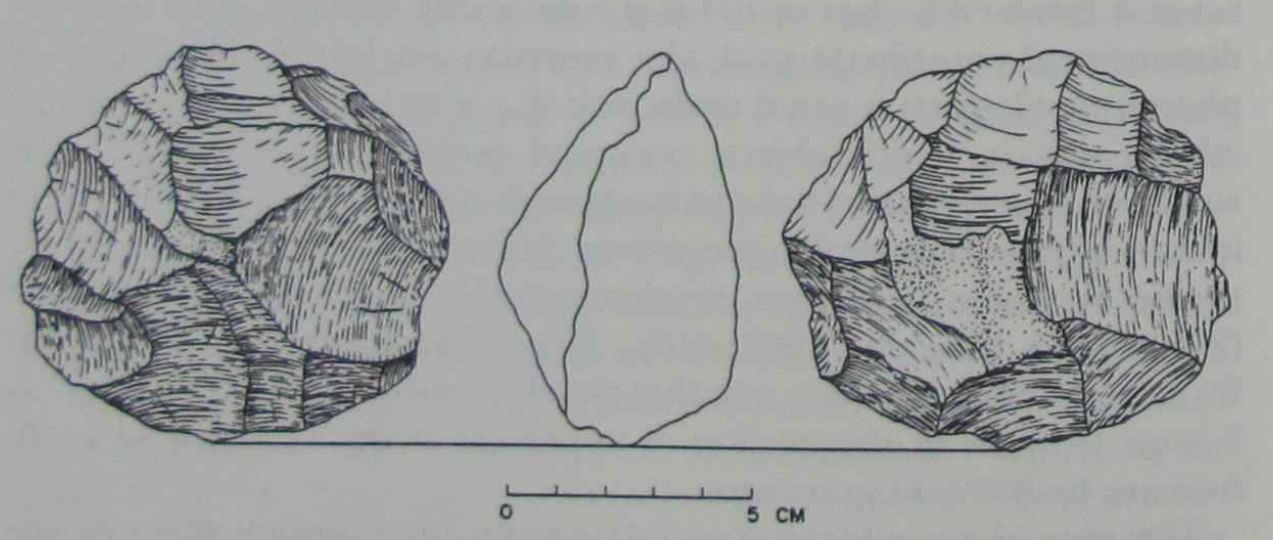 |
must have employed some additional spatial concept. At the minimum, he must have used some concept of radius or diameter, that is some notion of a constant amount of space separating all of the edges.
Alternatively, he might have used some idea of a regular curve employing a reference system of chords and arcs. But this is even more
complex than a radius. We may conclude that the knapper of this
discoid used some notion of interval, either radius or diameter, while
making this artifact. Again, I do not mean to argue that the knapper
was a geometrician and reflected upon such concepts, only that he
used a simple notion of interval in his spatial repertoire. |
Back to top: Euclidean concepts
Parallel axes
| Parallel axes and "affine" geometry |
p. 45 |
A second spatial notion that is an element of euclidean space is that
of parallel axes, which are essential to the formal definition of a coordinate grid. Actually, parallels constitute a geometry all their own,
termed "affine" geometry, with its own set of axioms and theorems.
While it is possible to define parallel lines using euclidean notions of
angles and measurement, it is not necessary to do so. Any two lines
on a plane that never meet are parallel. This definition assumes a
concept of plane, but in practice is well within the competence of an
intuitive geometry. This does not mean, however, that it must exist as
an independent notion in an intuitive conception of space, nor that it
must precede a truly euclidean geometry in a developmental sequence. |
| p. 48 |
This argument about affine geometry may appear, I admit, rather
like sophistry. But it does bear on two important aspects of our
problem – the antecedents of euclidean concepts and the relation between developmental and "logical" sequences. The lack of an affine
"stage" will turn out to be quite important. |
| Example |
p. 45 |
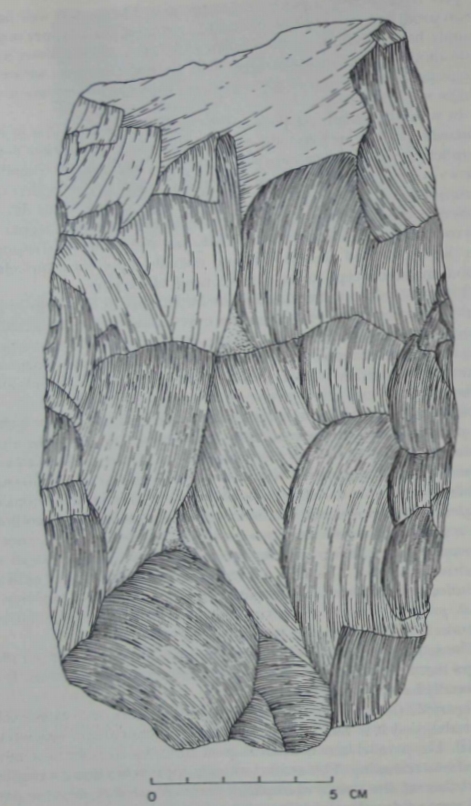
| Figure 22 (Isimila). The lateral edges of this cleaver are extensively
trimmed, and it is fair to assume that the overall shape was intentional. The parallel here is about as good as one could hope to achieve
by bifacial trimming. This artifact actually approaches being a regular
quadrilateral. But does it exemplify a notion of parallel, or is the parallel just a side effect of bilateral symmetry, which is not an affine
concept? |
 |
|
| Caveats |
p. 47 |
Based on artifacts such as these, an argument could be made that
the Isimila hominids had some concept of parallel in their spatial repertoire. However, there need not have been a concept of parallel that
was separate from euclidean notions of space since, as we shall see,
there are euclidean notions such as congruency that were used by the
Isimila hominids. To document a separate use of affine spatial relations, we would need an assemblage in which affine but not euclidean
relations were required. To my knowledge no such assemblage exists. |
Back to top: Euclidean concepts
Bilateral symmetry
| Definition |
p. 49 |
Bilateral symmetry in its strict sense is a euclidean concept. "Two
points are said to be symmetrical with respect to a point, P, if P bisects the line segment joining the two points. Two figures can be considered symmetrical with respect to a point (line) if each point in
one figure has a symmetrical point in the other drawing" [...] In the case of symmetry with respect
to a line (bilateral symmetry), the bisecting line must be perpendicular
to the segment joining any two symmetrical points. The notions of
"bisect" and "perpendicular" require the quantitative concepts of
angle and distance (concepts of rotational and linear measurement).
A simpler intuitive notion of symmetry consists of mirror images, one
an exact but reversed duplicate of the other. Yet even here the idea
of an exact duplicate usually means a congruency, which is of course
a euclidean notion requiring conserved amounts of space and angle. |
| Reversal and congruency |
p. 50 |
In this section I will examine the development of bilateral symmetry by citing examples of artifacts that required a reversal about a
perpendicular bisecting line (which I will simply term a midline) as
well as some notion of symmetrical congruency, that is, the theoretical
infinity of symmetrical points that constitute symmetrical figures. |
| Example |
p. 50f |
| An even more powerful argument for a concept of symmetry can
be based on minimally trimmed artifacts.
Figure 26 (Isimila). The trimming at A especially suggests attention
to mirroringa congruent shape. The bit has been "pulled in" for the
same distance on the retouched margin as it was naturally done on
the opposite margin. The subsequent constriction extends for the same length along each side. The knapper also trimmed the butt into |
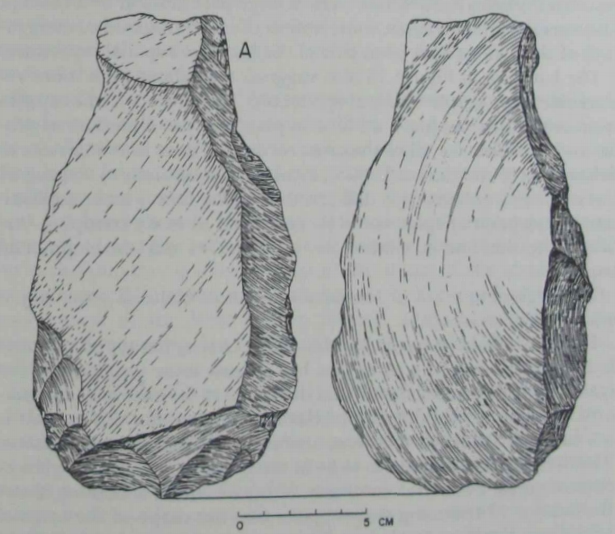 |
an even curve, giving the ardfact an excellent symmetry in plan with
minimal effort. The biface discussed earlier in Figure 7 presents a
similar approach to achieving symmetry. Both of these artifacts argue
for a concept of the relation between whole and parts. They also suggest that the conceived “whole” was in large part defined by a concept
of symmetry. In both cases, some notion of mirroring and of congruency of shape must have been part of the knapper’s spatial repertoire.
|


