Back to top: Projective concepts
Projective concepts
Definition:
constancy of items in spite of change in perspective |
p. 24 |
Projective geometry is a geometry of viewpoints or perspectives. It
is concerned with qualities of figures that remain constant when the
source of a projection changes. A simple way to explore projective
relations is to study changes in shadows cast by a point source such as
a candle or flashlight. One can easily transform the shadow of a
square piece of cardboard into a rhombus or a trapezoid, but it is impossible to change the shadow into a triangle or a circle. Some qualities of the figure remain constant regardless of its relation to the light
source. |
| Must be argued from within the object |
p. 25 |
We are interested
in intuitive notions of space and, in particular, in how these intuitive
notions govern the manufacture of stone tools. The intuitive notion
of perspective is therefore of some interest. Do any patterns displayed
by stone tools require concepts that include some consideration of
perspective, that is, that consider the relative orientation of object and
observer? [...] We are left
again with patterns internal to stone tools, and only a few of these
suggest specific projective notions. The most notable are intentional
straight edges and regular cross sections. |
| Must be argued from within the object |
p. 28 |
As is true of the topological concept of analysis and synthesis,
there is good evidence for consideration of perspective in later Acheulean bifaces. This competence included not only the ability to operate from one stable viewpoint but the ability to coordinate viewpoints. This conclusion is corroborated by the evidence from cross
sections. |
| MInimum necessary competence |
p. 33 |
Unless the artifact is extensively trimmed and extremely regular, it is difficult, if not impossible, to document projective relations. The minimum necessary
competence does not, therefore, include projective notions. |
Back to top: Projective concepts
Straight line
| Definition |
p. 25f. |
When the position of the observer is taken into account, certain
spatial qualities are added to the simpler topological ones. A straight
line viewed from the proper position becomes a point (the terminal
point of a straight line is capable of masking all of the other points),
but there is no position from which a curved line can be seen as a
point. The ability to create a straight line presupposes an awareness of this stable viewpoint, either by actual sighting or by imagination. [...] What is true of projective straight lines must also be true of straight
aspects of artifacts, but only if the straightness is clearly the result of
intentional modification. [...] Much that is straight on stone tools is a result
of manufacture on flakes, many of whose natural edges approach
straightness. |
Example:
|
p. 26 |
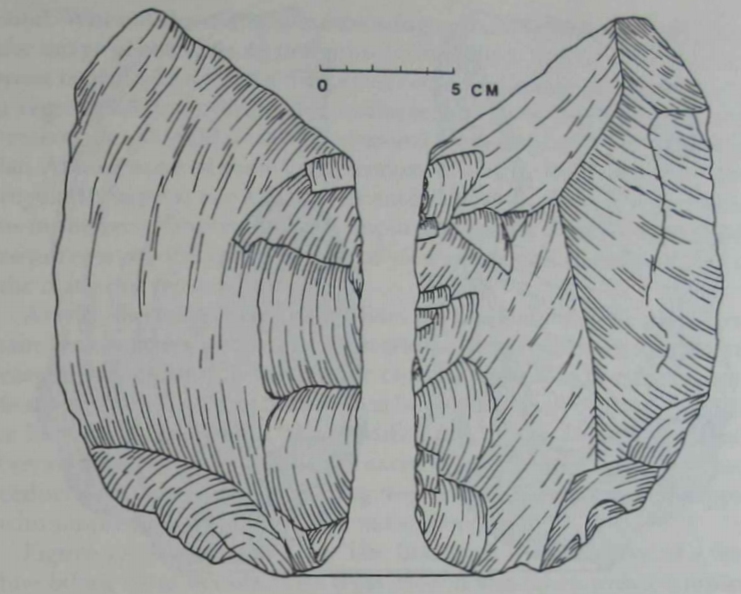
| The trimmed lateral edge of this
cleaver is remarkably straight, and, more important, the extent of the
trimming suggests that the original shape of the edge was considerably altered. The edge is also straight in profile. This required the
knapper to control two viewpoints or perspectives at the same time.
Competence in the basic topological notions discussed in the previous
chapter would not |
|
have been sufficient. The knapper had to have
related the trimming of the edge to a constant point of view. Moreover, because the edge is also straight in profile, the knapper had to
have considered a point of view located on another plane. Even if the
knapper continually checked the edge by actual sighting, he had to be
aware that the shape varied according to the viewpoint, that what was
straight from one sighting point was perhaps not straight from another. In other words, some notion of perspective must have been
present in the knapper's spatial repertoire, and a fairly sophisticated
one at that since there are two coordinated perspectives evident here.
|
Back to top: Projective concepts
Cross section
| Definition |
p. 28 |
The cross section of an object is the two-dimensional shape produced by a plane intersecting the solid. For example, the cross section
of a sphere is a circle; of a cylinder, a circle or an ellipse; of a pyramid,
a rectangle. The cross section of a biface is the two-dimensional shape
produced by an imaginary plane intersecting the artifact. We say that
a biface has a "regular" cross section if it presents a recognizable twodimensional figure such as a rhombus or a triangle or a lens shape.
Symmetry is usually the most telling quality of regularity. |
| Imagination |
p. 28f. |
The ability to conceive of and create a regular cross section requires
a sophisticated coordination of viewpoints or perspectives. First, it is
necessary that the observer – in our case the knapper – be aware of a
viewpoint that is not actually available to him. One cannot sight into a solid. Without the aid of some assisting apparatus such as a template the image of the cross section must be imagined.
Second, the observer must coordinate a virtual infinity of cross sections or perspectives. |
Example
|
p. 29 |
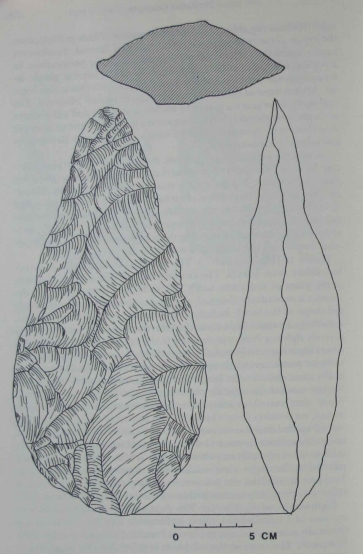
| The cross section was taken with a template
at the point of maximum width. As can be seen from Figure 13, the
artifact is extensively trimmed, and it is fair to conclude that the original shape of the blank, including the cross section, has been changed.
Could the knapper have controlled the shape of this cross section by
directly sighting from a perspective to the rear of the artifact? Such a
direct sighting would actually combine (and confound) the dimensions of maximum width and maximum thickness, which do not fall
at the same point on the length of the artifact (maximum thickness is
farther toward the tip). In other words, the knapper would see a
"view" that was a composite of two separate cross sections. |
|
There is,
in fact, no position from which the cross section of the artifact in Figure 13 can be directly observed. It must be created in the imagination
or, as I have done, measured with a device. Moreover, a planar intersection taken virtually anywhere on this artifact, even at angles not
parallel to the major axes, would yield a regular cross section. The
knapper constructed not just one imaginary viewpoint but a virtual
infinity of them. His control in this regard was quite remarkable.
|
| Reversal and congruency |
p. 51 |
[The item in Figure 13] is not only bilaterally symmetrical in plan, it is symmetrical
in profile and in all of its cross sections. Furthermore it is extensively
trimmed, and the shapes are certainly intentional. The symmetry is
extremely regular, and the mirrored shapes are congruent. One
could improve little on the result if one were to use a measuring device. The symmetries in this artifact come very close to fulfilling the
formal definition of symmetry. |
| End point of developmental sequence |
p. 52 |
The handaxe in Figure 13 also suggests something even more remarkable than simple bilateral symmetry. The artifact demonstrates
symmetry across not just a midline in plan, but also a midline in profile and a midline for all of the cross sections. These lines intersect to
define a three-dimensional space, intuitively equivalent to a space of
Cartesian coordinates. It is difficult to imagine how a more sophisticated conception of space could be employed in stone knapping. Artifacts like this one constitute the endpoint of our developmental
sequence. |
| Three-dimensional frame of reference |
p. 57 |
The fine bifaces, like those in example 13, have
bilateral symmetry in three dimensions (as we would define them).
The knapper had to be able to invert
congruent shapes across an
imaginary midline for three separate dimensions and to coordinate
them. This required a frame of reference of considerable complexity,
and, while I suppose it possible that this frame was applied only to
spatial relations on or within artifacts, this seems to me very unlikely.
The abstract nature of such a spatial framework suggests that it was a
general one, extendable to all of space. Again I must emphasize that
the knapper need not have been able to describe or to verbalize his
concepts in nice mathematical terms. That he employed such a framework, however, is, I think, undeniable. |

