Projective concepts

Giorgio Buccellati – October 2013

Projective concepts

Definition: constancy of items in spite of change in perspective	p. 24	Projective geometry is a geometry of viewpoints or perspectives. It is concerned with qualities of figures that remain constant when the source of a projection changes. A simple way to explore projective relations is to study changes in shadows cast by a point source such as a candle or flashlight. One can easily transform the shadow of a square piece of cardboard into a rhombus or a trapezoid, but it is impossible to change the shadow into a triangle or a circle. Some qualities of the figure remain constant regardless of its relation to the light source.
Must be argued from within the object	p. 25	We are interested in intuitive notions of space and, in particular, in how these intuitive notions govern the manufacture of stone tools. The intuitive notion of perspective is therefore of some interest. Do any patterns displayed by stone tools require concepts that include some consideration of perspective, that is, that consider the relative orientation of object and observer? [...] We are left again with patterns internal to stone tools, and only a few of these suggest specific projective notions. The most notable are intentional straight edges and regular cross sections.
Must be argued from within the object	p. 28	As is true of the topological concept of analysis and synthesis, there is good evidence for consideration of perspective in later Acheulean bifaces. This competence included not only the ability to operate from one stable viewpoint but the ability to coordinate viewpoints. This conclusion is corroborated by the evidence from cross sections.
MInimum necessary competence	p. 33	Unless the artifact is extensively trimmed and extremely regular, it is difficult, if not impossible, to document projective relations. The minimum necessary competence does not, therefore, include projective notions.

Straight line

Definition

p. 25f.

When the position of the observer is taken into account, certain spatial qualities are added to the simpler topological ones. A straight line viewed from the proper position becomes a point (the terminal point of a straight line is capable of masking all of the other points), but there is no position from which a curved line can be seen as a point. The ability to create a straight line presupposes an awareness of this stable viewpoint, either by actual sighting or by imagination. [...] What is true of projective straight lines must also be true of straight aspects of artifacts, but only if the straightness is clearly the result of intentional modification. [...] Much that is straight on stone tools is a result of manufacture on flakes, many of whose natural edges approach straightness.

Example:

p. 26

The trimmed lateral edge of this cleaver is remarkably straight, and, more important, the extent of the trimming suggests that the original shape of the edge was considerably altered. The edge is also straight in profile. This required the knapper to control two viewpoints or perspectives at the same time. Competence in the basic topological notions discussed in the previous chapter would not

have been sufficient. The knapper had to have related the trimming of the edge to a constant point of view. Moreover, because the edge is also straight in profile, the knapper had to have considered a point of view located on another plane. Even if the knapper continually checked the edge by actual sighting, he had to be aware that the shape varied according to the viewpoint, that what was straight from one sighting point was perhaps not straight from another. In other words, some notion of perspective must have been present in the knapper's spatial repertoire, and a fairly sophisticated one at that since there are two coordinated perspectives evident here.

Cross section

Definition

p. 28

The cross section of an object is the two-dimensional shape produced by a plane intersecting the solid. For example, the cross section of a sphere is a circle; of a cylinder, a circle or an ellipse; of a pyramid, a rectangle. The cross section of a biface is the two-dimensional shape produced by an imaginary plane intersecting the artifact. We say that a biface has a "regular" cross section if it presents a recognizable twodimensional figure such as a rhombus or a triangle or a lens shape. Symmetry is usually the most telling quality of regularity.

Imagination

p. 28f.

The ability to conceive of and create a regular cross section requires a sophisticated coordination of viewpoints or perspectives. First, it is necessary that the observer – in our case the knapper – be aware of a viewpoint that is not actually available to him. One cannot sight into a solid. Without the aid of some assisting apparatus such as a template the image of the cross section must be imagined. Second, the observer must coordinate a virtual infinity of cross sections or perspectives.

Example

p. 29

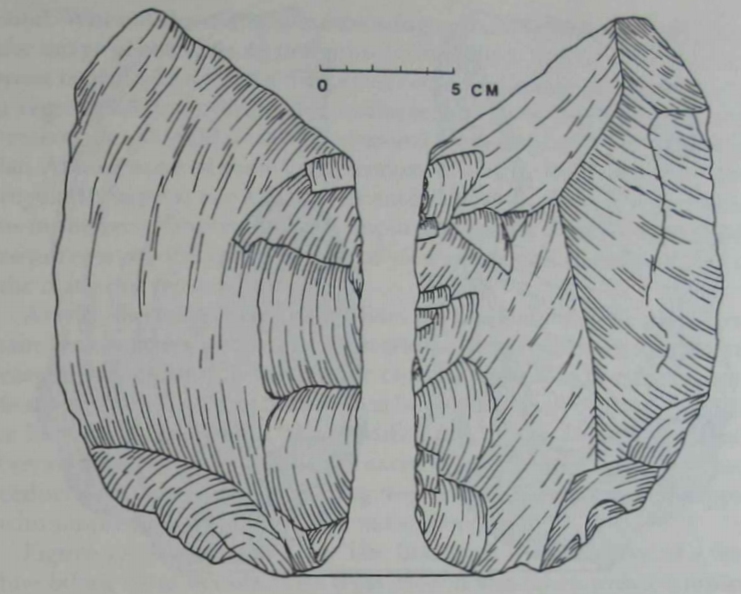
The cross section was taken with a template at the point of maximum width. As can be seen from Figure 13, the artifact is extensively trimmed, and it is fair to conclude that the original shape of the blank, including the cross section, has been changed. Could the knapper have controlled the shape of this cross section by directly sighting from a perspective to the rear of the artifact? Such a direct sighting would actually combine (and confound) the dimensions of maximum width and maximum thickness, which do not fall at the same point on the length of the artifact (maximum thickness is farther toward the tip). In other words, the knapper would see a "view" that was a composite of two separate cross sections.

There is, in fact, no position from which the cross section of the artifact in Figure 13 can be directly observed. It must be created in the imagination or, as I have done, measured with a device. Moreover, a planar intersection taken virtually anywhere on this artifact, even at angles not parallel to the major axes, would yield a regular cross section. The knapper constructed not just one imaginary viewpoint but a virtual infinity of them. His control in this regard was quite remarkable.

Reversal and congruency

p. 51

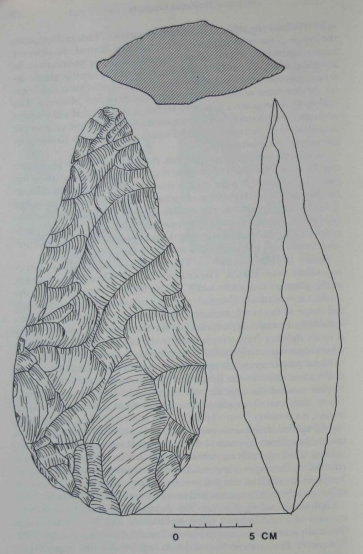
[The item in Figure 13] is not only bilaterally symmetrical in plan, it is symmetrical in profile and in all of its cross sections. Furthermore it is extensively trimmed, and the shapes are certainly intentional. The symmetry is extremely regular, and the mirrored shapes are congruent. One could improve little on the result if one were to use a measuring device. The symmetries in this artifact come very close to fulfilling the formal definition of symmetry.

End point of developmental sequence

p. 52

The handaxe in Figure 13 also suggests something even more remarkable than simple bilateral symmetry. The artifact demonstrates symmetry across not just a midline in plan, but also a midline in profile and a midline for all of the cross sections. These lines intersect to define a three-dimensional space, intuitively equivalent to a space of Cartesian coordinates. It is difficult to imagine how a more sophisticated conception of space could be employed in stone knapping. Artifacts like this one constitute the endpoint of our developmental sequence.

Three-dimensional frame of reference

p. 57

The fine bifaces, like those in example 13, have bilateral symmetry in three dimensions (as we would define them). The knapper had to be able to invert congruent shapes across an imaginary midline for three separate dimensions and to coordinate them. This required a frame of reference of considerable complexity, and, while I suppose it possible that this frame was applied only to spatial relations on or within artifacts, this seems to me very unlikely. The abstract nature of such a spatial framework suggests that it was a general one, extendable to all of space. Again I must emphasize that the knapper need not have been able to describe or to verbalize his concepts in nice mathematical terms. That he employed such a framework, however, is, I think, undeniable.